east (Euler'south Number)

e (eulers number)

The number e is 1 of the most important numbers in mathematics.

The get-go few digits are:

2.7182818284590452353602874713527 (and more ...)

Information technology is often chosen Euler'southward number after Leonhard Euler (pronounced "Oiler").

e is an irrational number (it cannot exist written as a simple fraction).

e is the base of operations of the Natural Logarithms (invented by John Napier).

e is constitute in many interesting areas, so is worth learning almost.

Calculating

In that location are many ways of calculating the value of e , but none of them ever give a totally exact respond, because due east is irrational and its digits go on forever without repeating.

Just it is known to over ane trillion digits of accuracy!

For instance, the value of (1 + one/due north)north approaches east equally north gets bigger and bigger:

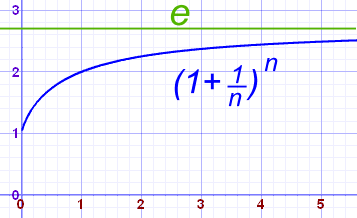
graph of (1+1/n)^n

n (1 + i/n)n
1 two.00000
ii 2.25000
five 2.48832
10 2.59374
100 2.70481
1,000 2.71692
ten,000 ii.71815
100,000 2.71827

Endeavour it! Put "(i + 1/100000)^100000" into the computer:

(1 + ane/100000)100000

What do you become?

Some other Calculation

The value of e is also equal to 1 0! + 1 1! + one two! + 1 3! + 1 4! + one five! + 1 6! + 1 vii! + ... (etc)

(Annotation: "!" means factorial)

The first few terms add upwards to: 1 + i + 1 two + i 6 + 1 24 + 1 120 = 2.71666...

In fact Euler himself used this method to calculate due east to 18 decimal places.

Y'all can try information technology yourself at the Sigma Calculator.

Remembering

To remember the value of e (to 10 places) just remember this saying (count the letters!):

  • To
  • express
  • e
  • remember
  • to
  • memorize
  • a
  • sentence
  • to
  • memorize
  • this

Or you can retrieve the curious pattern that after the "2.7" the number "1828" appears TWICE:

2.seven 1828 1828

And following THAT are the digits of the angles 45°, xc°, 45° in a Right-Angled Isosceles Triangle (no real reason, just how information technology is):

2.vii 1828 1828 45 90 45

(An instant way to seem really smart!)

Growth

e is used in the "Natural" Exponential Function:

natural exponential function
Graph of f(10) = ex

It has this wonderful property: "its slope is its value"

At whatsoever point the slope of e 10 equals the value of e x :

natural exponential function
when x=0, the value east x = ane , and the slope = 1
when x=i, the value east x = due east , and the slope = e
etc...

This is truthful anywhere for e x, and helps us a lot in Calculus when we demand to find slopes etc.

So due east is perfect for natural growth, come across exponential growth to larn more.

Surface area

The area upwardly to any x-value is likewise equal to e x :

natural exponential function

An Interesting Property

Just for fun, attempt "Cut Up So Multiply"

Let united states say that we cut a number into equal parts and then multiply those parts together.

Example: Cut ten into 2 pieces and multiply them:

Each "slice" is 10/ii = 5 in size

5×5 = 25

At present, ... how could we get the reply to be as big as possible, what size should each piece be?

The answer: make the parts as close as possible to " e " in size.

Example: 10

x cutting into 2 equal parts is 5: 5×5 = 5two = 25

ten cut into 3 equal parts is iii 1 iii : (3 1 three )×(3 1 3 )×(3 one 3 ) = (iii ane three )3 = 37.0...

10 cut into 4 equal parts is 2.5: two.five×two.5×two.5×2.5 = 2.54 = 39.0625

x cutting into 5 equal parts is 2: 2×ii×2×2×2 = ii5 = 32

The winner is the number closest to " e ", in this example 2.5.

Try information technology with another number yourself, say 100, ... what exercise y'all go?

100 Decimal Digits

Here is due east to 100 decimal digits:

2.71828182845904523536028747135266249775724709369995957
49669676277240766303535475945713821785251664274...

Advanced: Use of e in Compound Interest

Often the number e appears in unexpected places. Such as in finance.

Imagine a wonderful bank that pays 100% interest.

In 1 twelvemonth you could turn $1000 into $2000.

Now imagine the bank pays twice a year, that is 50% and 50%

Half-style through the twelvemonth you lot have $1500,
you reinvest for the remainder of the year and your $1500 grows to $2250

You got more coin, because you reinvested half way through.

That is chosen compound involvement.

Could we become even more if nosotros bankrupt the yr upwards into months?

Nosotros can use this formula:

(one+r/north)due north

r = almanac interest rate (as a decimal, so 1 not 100%)
n = number of periods inside the yr

Our half yearly example is:

(1+ane/2)2 = ii.25

Let's effort information technology monthly:

(1+ane/12)12 = ii.613...

Let's try it 10,000 times a yr:

(ane+i/10,000)10,000 = 2.718...

Yep, it is heading towards e (and is how Jacob Bernoulli first discovered it).

Why does that happen?

The answer lies in the similarity betwixt:

Compounding Formula: (1 + r/n)north
and
e (as n approaches infinity): (one + 1/northward)n

The Compounding Formula is very like the formula for e (every bit n approaches infinity), simply with an extra r (the interest rate).

When we chose an interest rate of 100% (= 1 as a decimal), the formulas became the same.

Read Continuous Compounding for more.

Euler'southward Formula for Complex Numbers

east also appears in this virtually astonishing equation:

e i π + 1 = 0

Read more here

Transcendental

east is also a transcendental number.

e-Day

balloons

Celebrate this astonishing number on

  • 27th Jan: 27/ane at viii:28 if you like writing your days first, or
  • February 7th: 2/7 at eighteen:28 if y'all like writing your months first, or
  • On both days!

2011, 2012, 2013